Razones trigonométricas inversas[editar]
- La Cosecante: (abreviado como csc o cosec) es la razón inversa de seno, o también su inverso multiplicativo:
En el esquema su representación geométrica es:
- La Secante: (abreviado como sec) es la razón inversa de coseno, o también su inverso multiplicativo:
En el esquema su representación geométrica es:
- La Cotangente: (abreviado como cot o cta o ctg) es la razón inversa de la tangente, o también su inverso multiplicativo:
En el esquema su representación geométrica es:
Normalmente se emplean las relaciones trigonométricas seno, coseno y tangente, y salvo que haya un interés específico en hablar de ellos o las expresiones matemáticas se simplifiquen mucho, los términos cosecante, secante y cotangente no suelen utilizarse
Representación gráfica[editar]
Otras funciones trigonométricas[editar]
Además de las funciones anteriores, existen otras funciones trigonométricas. Matemáticamente se pueden definir empleando las ya vistas. Su uso no es muy corriente, pero sí se emplean, dado su sentido geométrico. Veamos:
El seno cardinal o función sinc (x) definida:
El verseno, es la distancia que hay entre la cuerda y el arco en una circunferencia, también se denomina sagita o flecha, se define:
El semiverseno, se utiliza en navegación al intervenir en el cálculo esférico:
El coverseno,
El semicoverseno
La exsecante:
Funciones trigonométricas recíprocas[editar]
En trigonometría, cuando el ángulo se expresa en radianes (dado que un radián es el arco de circunferencia de longitud igual al radio), suele denominarse arco a cualquier cantidad expresada en radianes; por eso las funciones recíproca se denominan con el prefijo arco, cada razón trigonométrica posee su propia función recíproca:
y es igual al seno de x, la función recíproca:
x es el arco cuyo seno vale y, o también x es el arcoseno de y.
si:
y es igual al coseno de x, la función recíproca:
x es el arco cuyo coseno vale y, que se dice: x es el arcocoseno de y.
si:
y es igual al tangente de x, la función recíproca:
x es el arco cuya tangente vale y, o x es igual al arcotangente de y.
NOTA: Es común, que las funciones recíprocas sean escritas de esta manera:
pero se debe tener cuidado de no confundirlas con:
Representación gráfica[editar]
Si aplicamos el criterio para obtener las funciones recíprocas en el sentido estricto, definiendo el arcoseno como la recíproca del seno, el arcocoseno como la recíproca del coseno y el arco tangente como la recíproca de la tangente, lo obtenido es la gráfica de la derecha. Es fácil percatarse que estas representaciones no cumplen la unicidad de la imagen, que forma parte de la definición de función, eso es para un valor de x dado existen un número infinito de valore que son su función, por ejemplo: el arcoseno de 0 es 0, pero también lo son cualquier múltiplo entero de  .
.
 .
.
Para cualquier n número entero.
Dado que la recíproca de una función no tiene que cumplir necesariamente la unicidad de imagen, solo la funciones inyectivas y biyectivas dan funciones recíprocas con esta propiedad, esta situación se repite para el resto de las funciones recíprocas trigonométricas.
A fin de garantizar el cumplimiento de la definición de función, en cuanto a la unicidad de imagen, y que por tanto las funciones trigonométricas recíprocas cumplan los criterios de la definición de función, se suele restringir tanto el dominio como el codominio, esta corrección permite un análisis correcto de la función, a pesar de que no coincida exactamente con la reciproca de la función trigonométrica original. Así tenemos que:
La función arcoseno se define:
La función arcocoseno se define:
La función arcotangente se define:
Esta restricción garantiza el cumplimiento de la definición de función, en cuanto a la existencia y unicidad de la imagen, si bien tiene inconvenientes como el no poder comparar el arcoseno y el arcocoseno al estar definidos en codominios diferentes, o el de presentar discontinuidades inexistentes, tanto si se emplean las funciones trigonométricas reciprocas en su forma directa como corregida se ha de ser consciente de ello, y comprender las ventajas e inconvenientes que esto supone.

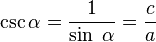
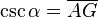
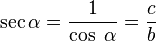
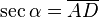

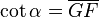







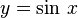

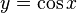

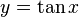






![\begin{array}{rccl}
\arcsin : & [-1,1] & \to & [-0,5 \pi \; , \; 0,5 \pi] \\
& x & \to & y = \arcsin(x)
\end{array}](https://upload.wikimedia.org/math/9/1/3/913067c1335c60a696f2519b75d33db2.png)
![\begin{array}{rccl}
\arccos : & [-1,1] & \to & [0 \; , \; \pi] \\
& x & \to & y = \arccos(x)
\end{array}](https://upload.wikimedia.org/math/f/1/4/f1465bc918a1e975824ff501b196873d.png)
![\begin{array}{rccl}
\arctan : & R & \to & [-0,5 \pi \; , \; 0,5 \pi] \\
& x & \to & y = \arctan(x)
\end{array}](https://upload.wikimedia.org/math/3/9/e/39e54a9da29bc7be9543af66566df72e.png)
No hay comentarios:
Publicar un comentario