trigonometria: funciones trigonométricas inversas reciprocas

Funciones trigonométricas inversas recíprocas[editar]

Del mismo modo que las funciones trigonométricas directas recíprocas, cuando el ángulo se expresa en radianes, se denomina arco a ese ángulo, y se emplea el prefijo arco para la función trigonométrica recíproca, así tenemos que:

y= \csc \, x \,

y es igual a la cosecante de x, la función recíproca:

x = \arccsc \; y \,

x es el arco cuya cosecante vale y, o también x es la arcocosecante de y.

si:

y= \sec x \,

y es igual al secante de x, la función recíproca:

x = \arcsec y \,

x es el arco cuya secante vale y, que se dice: x es el arcosecante de y.

si:

y= \cot x \,

y es igual al cotangente de x, la función recíproca:

x = \arccot y \,

x es el arco cuya cotangente vale y, o x es igual al arcocotangente de y.

Representación gráfica[editar]

Representación de las funciones trigonométricas inversas reciprocas en el plano cartesiano (x,y), como la recíproca de la cosecante, secante y cotangente, los valores en el eje y expresados en radianes.

Al igual que en las funciones directas, si aplicamos el criterio para obtener las funciones recíprocas, dado que las funciones trigonométricas inversas no son inyectivas, lo obtenido es la gráfica de la derecha, que no cumplen la unicidad de la imagen, que forma parte de la definición de función.

Representación de las funciones trigonométricas inversas reciprocas, corregidas.

Para que se cumpla la definición de función, definimos un dominio y un codominio restrijido. Así tenemos que:

La función arcocosecante se define:

\begin{array}{rccl} \arccsc : & (-\infty , -1] \cup [1 , \infty) & \to & [-0,5 \pi \; , \; 0,5 \pi] \\ & x & \to & y = \arccsc(x) \end{array}

La función arcosecante se define:

\begin{array}{rccl} \arcsec : & (-\infty , -1] \cup [1 , \infty) & \to & [0 \; , \; \pi] \\ & x & \to & y = \arcsec(x) \end{array}

La función arcocotangente se define:

\begin{array}{rccl} \arccot : & R & \to & [0 \; , \; \pi] \\ & x & \to & y = \arccot(x) \end{array}

Esta restricción garantiza el cumplimiento de la definición de función.

Equivalencia entre las funciones trigonométricas[editar]

	Seno	Coseno	Tangente	Cotangente	Secante	Cosecante
$\sin\theta\,$	$\sin\theta\,$	$\sqrt{1-\cos^{2}\theta}$	$\frac{\tan\theta}{\sqrt{1+\tan^{2}\theta}}$	$\frac{1}{\sqrt{1+\cot^{2}\theta}}$	$\frac{\sqrt{\sec^{2}\theta-1}}{\sec\theta}$	$\frac{1}{\csc\theta}$
$\cos\theta\,$	$\sqrt{1-\sin^{2}\theta}$	$\cos\theta\,$	$\frac{1}{\sqrt{1+\tan^{2}\theta}}$	$\frac{\cot\theta}{\sqrt{1+\cot^{2}\theta}}$	$\frac{1}{\sec\theta}$	$\frac{\sqrt{\csc^{2}\theta-1}}{\csc\theta}$
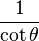$\tan\theta\,$	$\frac{\sin\theta}{\sqrt{1-\sin^{2}\theta}}$	$\frac{\sqrt{1-\cos^{2}\theta}}{\cos\theta}$	$\tan\theta\,$	$\frac{1}{\cot\theta}$	$\sqrt{sec^{2}\theta-1}$	$\frac{1}{\sqrt{\csc^{2}\theta-1}}$
$\cot\theta\,$	$\frac{\sqrt{1-\sin^{2}\theta}}{\sin\theta}$	$\frac{\cos\theta}{\sqrt{1-\cos^{2}\theta}}$	$\frac{1}{\tan\theta}$	$\cot\theta\,$	$\frac{1}{\sqrt{\sec^{2}\theta-1}}$	$\sqrt{\csc^{2}\theta-1}$
$\sec\theta\,$	$\frac{1}{\sqrt{1-\sin^{2}\theta}}$	$\frac{1}{\cos\theta\,}$	$\sqrt{1+\tan^{2}\theta}$	$\frac{\sqrt{1+\cot^{2}\theta}}{\cot\theta}$	${\sec\theta}\,$	$\frac{\csc\theta}{\sqrt{\csc^{2}\theta-1}}$
$\csc\theta\,$	$\frac{1}{\sin\theta\,}$	$\frac{1}{\sqrt{1-\cos^{2}\theta}}$	$\frac{\sqrt{1+\tan^{2}\theta}}{\tan\theta}$	$\sqrt{1+\cot^{2}\theta}$	$\frac{\sec\theta}{\sqrt{\sec^{2}\theta-1}}$	${\csc\theta}\,$